Věta o pizze (koláčku)
Publikováno: 05. 05. 2014 | Autor: Eduard Šubert
Víte jak správně rozdělit pizzu mezi dva jedlíky? Nakrájíte ji na 8 dílků a každému dáte 4. Ale co když se Vám ji nepodaří nakrájet přesně? Pomůže Vám věta o pizze. Ve videu se můžete podívat na to, jak všechno funguje. Pokud si chcete řádně prostudovat celý důkaz, přečtěte si tento článek.
Inspiraci na toto video jsme čerpali na webu MadMath v článku Pizza – Solution
Pomocné lemma
Nejprve si dokážeme užitečný vztah mezi kolmými průvodiči:
\(|AP|^2 + |BP|^2 + |CP|^2 + |DP|^2 = 4R^2\)
Náčrtek k pomocnému lemmatu
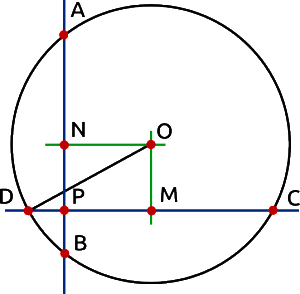
Vyjdeme z pravoúhlého trojúhelníku \(OMD\). Z Pythagorovy věty dostaneme vztah:
\( |OD|^2 = |MD|^2 + |OM|^2\)
Vyjádříme si vztahy pro \(|OM|\) a \(|MD|\):
\(|MD| = \frac{|CD|}{2} = \frac{|CP| + |PD|}{2}\)
\(|OM| = |NB| – |PB| = \frac{|PA|+|PB|}{2} – |PB| = \frac{|PA| – |PB|}{2}\)
A z těchto vztahů dosadíme:
\( |OD|^2 = \left(\frac{|CP| + |PD|}{2}\right)^2 + \left(\frac{|PA| – |PB|}{2}\right)^2 = |PA|^2 + |PB|^2 + |PC|^2 + |PD|^2 + 2\left(|PC||PD| – |PA||PB|\right)\)
Nyní stačí dokázat, že \(|PC||PD| – |PA||PB| = 0\) a důkaz pomocného lemmatu bude dokončen.
Označme souřadnice bodu \(P = [p_1,p_2]\). Z rovnice kružnice \(x^2+y^2=R^2\) vyjádříme funkci pro vrchní oblouk \(y=\sqrt{R^2-x^2}\).
\(|PA| = \sqrt{|OD|^2 – p_1^2} – p_2\)
\(|PB| = \sqrt{|OD|^2 – p_1^2} + p_2\)
\(|PC| = \sqrt{|OD|^2 – p_2^2} – p_1\)
\(|PD| = \sqrt{|OD|^2 – p_2^2} + p_1\)
Z těchto vztahů už snadno dokončíme důkaz:
\(|PC||PD| = \left(\sqrt{|OD|^2 – p_1^2} – p_2\right)\left(\sqrt{|OD|^2 – p_1^2} + p_2\right)\\ = |OD|^2 – p_1^2 – p_2^2 = \left(\sqrt{|OD|^2 – p_2^2} – p_1\right)\left(\sqrt{|OD|^2 – p_2^2} + p_1\right) = |PA||PB|\)
Pro další pokračování si označíme \(|PA| = a\), \(|PB| = b\), \(|PC| = c\), \(|PD| = d\) a \(|OD| = R\). Z právě dokázaného vztahu tak vznikne:
\(a^2 + b^2 + c^2 + d^2 = 4R^2\)
Věta o pizze
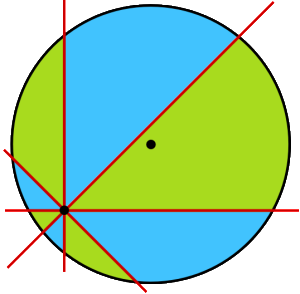
Když rozkrájíme pizzu čtyřmi řezy (nový řez vznikne rotací předchozího o 45°) protínajícími se v jednom bodě uvnitř pizzy a dílky rozdělíme střídavě mezi dva jedlíky, oba sní stejnou část pizzy.
Dle věty o pizze se obsahy zelené a modré části rovnají.
Rovnost obsahů obou ploch ověříme integrací, zaveďme tedy funkce \(a(\varphi)\), \(b(\varphi)\), \(c(\varphi)\) a \(d(\varphi)\) určující délku čtyř kolmých průvodičů z průsečíku řezů. Plochu jednoho dílku bychom tak určili:
\(\int_0^\frac{\pi}{4} \int_0^{a(\varphi)} r \text{d}r\text{d}\varphi = \int_0^\frac{\pi}{4} \frac{\left(a(\varphi)\right)^2}{2} \text{d}\varphi\)
Jelikož neznáme průběh funkce \(a(\varphi)\) nemůžeme určit obsah jednoho dílku, to ale nevadí, protože chceme znát obsah celé zelené části.
\(\int_0^\frac{\pi}{4} \frac{\left(a(\varphi)\right)^2}{2} + \frac{\left(b(\varphi)\right)^2}{2} + \frac{\left(c(\varphi)\right)^2}{2} + \frac{\left(d(\varphi)\right)^2}{2} \text{d}\varphi\)
Na součet délek průvodičů aplikujeme dříve dokázané lemma:
\(\int_0^\frac{\pi}{4} \frac{\left(a(\varphi)\right)^2}{2} + \frac{\left(b(\varphi)\right)^2}{2} + \frac{\left(c(\varphi)\right)^2}{2} + \frac{\left(d(\varphi)\right)^2}{2} \text{d}\varphi = \int_0^\frac{\pi}{4} \frac{4R^2}{2} = \int_0^\frac{\pi}{4} 2R^2 = \frac{R^2\pi}{2}\)
Stejným způsobem určíme i plochu modré části, tentokrát budeme integrovat přes jiné meze:
\(\int_\frac{\pi}{4}^\frac{\pi}{2} \frac{\left(a(\varphi)\right)^2}{2} + \frac{\left(b(\varphi)\right)^2}{2} + \frac{\left(c(\varphi)\right)^2}{2} + \frac{\left(d(\varphi)\right)^2}{2} \text{d}\varphi = \int_\frac{\pi}{4}^\frac{\pi}{2} \frac{4R^2}{2} = \int_\frac{\pi}{4}^\frac{\pi}{2}{4} 2R^2 = 2R^2\left( \frac{\pi}{2} – \frac{\pi}{4} \right) = \frac{R^2\pi}{2}\)
Hned vidíme, že se obsahy obou ploch rovnají, věta je tak dokázána.
Zobecnění
Větu lze dokázat i pro \(4n, (n>1)\) dílků. Tedy pro 8, 12, 16 a tak dále.